이등변삼각형의 성질
- 이등변삼각형이란, 두 변의 길이가 같은 삼각형이다.
- 특히, 이등변삼각형의 두 밑각의 크기가 같다.
- 다시 말해, 삼각형에서 두 변의 길이가 같으면 두 변과 마주보는 각의 크기도 같다. 왜 그럴까?
증명을 향한 여러 가지 길
- 이등변삼각형의 성질을 증명하기 위해서는 길이가 같은 두 변과 마주보는 두 각의 크기가 같음을 밝히면 된다.
- 이런 경우 삼각형의 합동조건이라는 도구를 사용할 수 있다.
- 그런데 주어진 삼각형이라곤 이등변삼각형 자기자신 즉, 하나뿐이다. 어떻게 할까?
- 이등변삼각형을 합동이 되는 두 삼각형으로 자를 수 있다.
- 이때, 두 변의 길이가 같다는 조건을 활용하기 위해서는 꼭지각의 꼭짓점을 지나면서 잘라야한다.
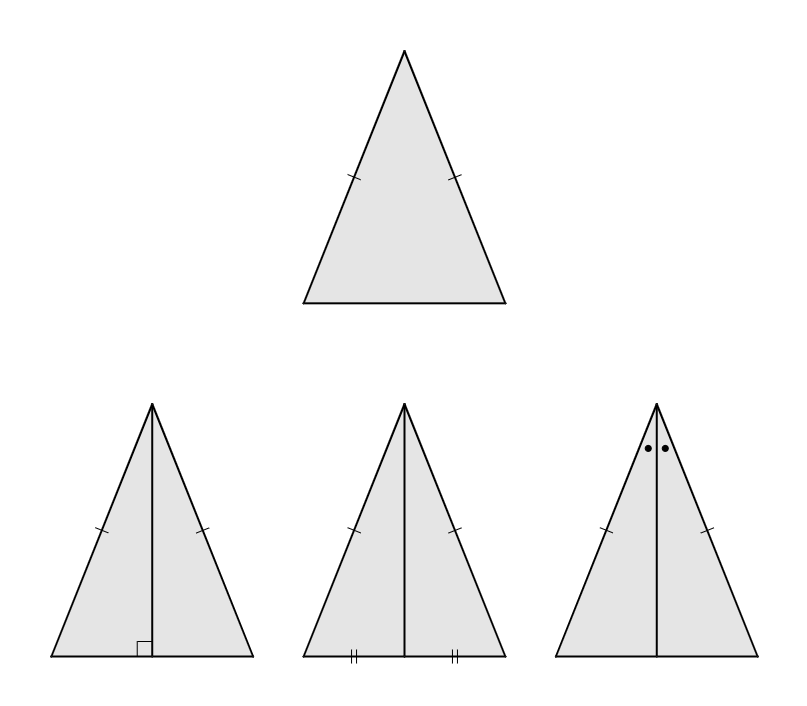
- 이제 이등변삼각형의 꼭지각의 꼭짓점에서 출발하여 여러 가지 길로 증명해보자.
- 꼭지각의 꼭짓점에서 밑변 위로 수선의 발을 내린다.
- 꼭지각의 꼭짓점에서 중선을 그린다.
- 꼭지각의 이등분선을 그린다.
