베르트랑의 역설 with AlgeoMath
베르트랑의 역설 with Desmos
베르트랑의 역설
한 원과 그 원에 내접한 정삼각형이 있다.
무작위로 한 현을 선택할 때, 그 현이 원에 내접한 정삼각형의 한 변 보다 길 확률은 얼마일까?
베르트랑은 이 확률을 구하는 세 가지 방법을 소개했는데, 이 방법은 모두 타당하면서도 결과 즉, 확률은 모두 다르다. 세 가지 방법은 다음과 같다.
- 원 위에서 두 점을 무작위로 고른다. 이제 두 점을 끝점으로 하는 선분을 현으로 선택한다.
- 원의 반지름을 하나 무작위로 고른다. 그리고 반지름에서 한 점을 무작위로 고른다. 이제 이 점을 중점으로 하는 현을 선택한다.
- 원의 내부에서 한 점을 무작위로 고른다. 그리고 이 점을 중점으로 하는 현을 선택한다.
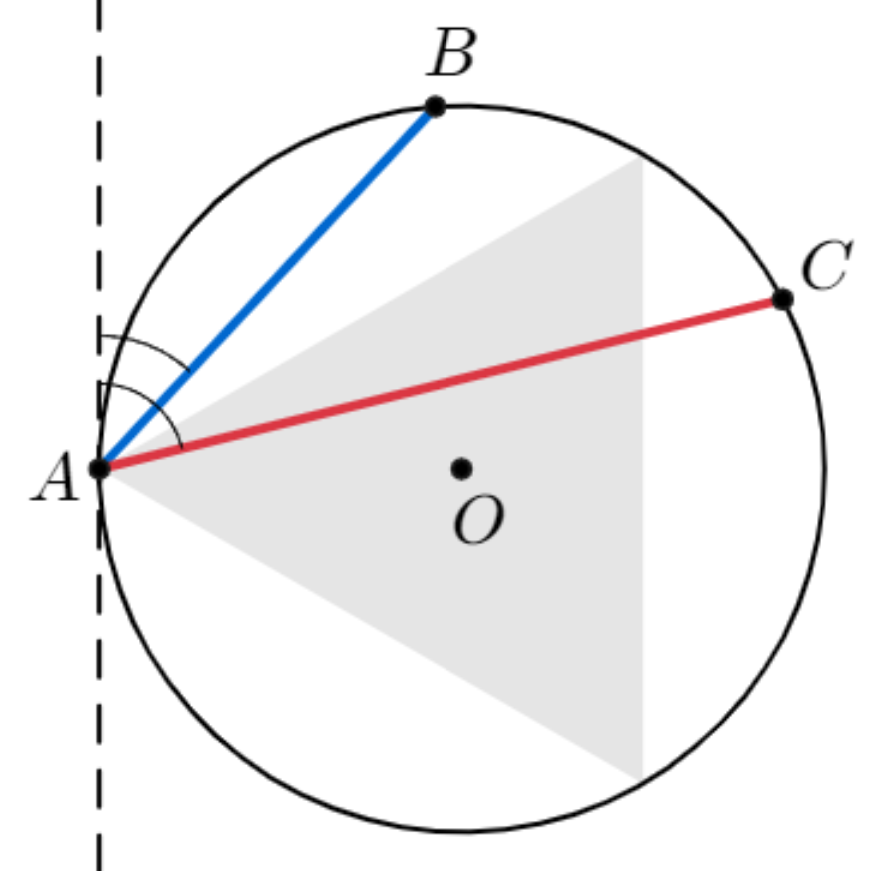 |
 |
 |
| 현의 한 끝점과 그 점의 접선과의 각의 크기가 60° 보다 크고 120°m; 보다 작을 때, 현이 정삼각형의 한 변 보다 길다. 따라서, 확률은 1/3 이다. | 반지름 위에서 고른 점이 중심에 반지름 길이의 절반 보다 가까이 있을 때, 현이 정삼각형의 한 변 보다 길다. 따라서, 확률은 1/2 이다. | 원의 내부에서 고른 점이 정삼각형의 내접원의 내부에 있을 때, 현이 정삼각형의 한 변 보다 길다. 따라서, 확률은 두 원의 넓이 비인 1 : 4 즉, 1/4 이다. |
설명
- 베르트랑의 역설은 확률 개념의 발달 과정의 논쟁이 되었던 유명한 패러독스로 잘 알려져 있다.
- 모든 선분을 '선분 만들기' 블록으로 만들면, 개수가 늘어날수록 실행속도가 크게 줄어들다가 웹브라우저가 멈추는 문제가 있다.
- 이 문제를 해결하기 위해 처음에 선분을 하나만 만들고 이 선분이 자취를 남기며 이동하게 했다.
- 그럼에도 현의 개수가 늘어날수록 실행속도가 줄어드는 문제점은 피할수가 없다.
참고
- en.wikipedia.org/wiki/Bertrand_paradox_(probability)
- 배움&창작(2018). 베르트랑의 현 #1 with AlgeoMath.
- 배움&창작(2018). 베르트랑의 현 #2 with AlgeoMath.
- 배움&창작(2018). 베르트랑의 현 #3 with AlgeoMath.
