2014년 1월 21일에 작성한 텀블러 포스트이다.
- 제목: 학문의 즐거움
- 원제: 学問の発見
- 저자: 広中平祐 (ひろなか へいすけ)
- 역자: 방승양
- 출판: 김영사
이 책의 54 페이지에 다음과 같은 기하 문제가 있다.
그런데 고등학교 시절에 장시간 걸려서 푼 문제 중에 지금까지 잊혀지지 않는 것이 있다. 그것은 다음과 같은 기하 문제이다.
삼각형의 두 밑각을 각각 이등분하는 선을 그려서, 각 선이 대변에 교차하는 점까지의 길이가 같을 때 이 삼각형이 이등변삼각형임을 증명하여라.
이 문제는 삼각함수를 쓰면 쉽게 풀 수 있지만 당시는 삼각함수를 배우기 전이었으므로 내게는 난제 중에 난제였다.
난 2주일 동안 다른 공부에는 일체 손을 대지 않고, 밥 먹을 때나 화장실을 갈 때나 이 문제를 푸는 데만 열중했다. 결국은 서너 가지의 경우로 나누어 증명할 수가 있었다.
나는 삼각함수를 쓰면 쉽게 풀린다는 저자의 말을 사인법칙이나 코사인법칙으로 '직접 증명' 할 수 있다는 말로 생각하고 정말 여러가지로 다양하게 몇 시간에 걸쳐 풀려고 해봤으나 풀리지 않았다. 내 참을성이 저자에 비해 너무 부족해서 몇 분 정도 구글링을 했더니 영문 위키에서 Steiner-Lehmus theorem을 찾을 수 있었다. 그 양이 많지 않아서 전문을 옮겨 봤다.
스타이너-리무스 정리 (Steiner-Lehmus theorem)
초등 기하학에서 스타이너-리무스 정리는 리무스(C. L. Lehmus)에 의하여 고안되었고, 이어서 야콥 스타이너(Jakob Steiner)에 의해 증명되었다.
두 각의 이등분선의 길이가 같은 임의의 삼각형은 이등변삼각형이다.
정리는 1840년에 리무스가 스튀름에게 순수한 기하학적 증명을 물었던 편지에서 처음으로 언급되었다. 스튀름은 이를 다른 수학자들에게 알렸고, 그 중에서 스타이너가 처음으로 해답을 제시했다. 이 정리는 몇몇 정기적인 출판물에 실린 이후로 줄곧 초등 기하학의 꽤나 유명한 주제가 되었다.
직접 증명 (Direct proofs)
이 정리는 본 명제의 대우를 초등 기하학으로 이용하여 증명함으로써 증명될 수 있다. '직접적인' 증명이 가능한지에 대해서는 약간의 논쟁이 있다. 전해지는 바에 의하면 직접 증명이 알려졌다고 하지만 모든 사람들이 그것의 직접성에 동의하는 것은 아니다.
예를 들어, 삼각형의 세 변의 길이를 이용한 각의 이등분선의 단순한 대수식이 있다. 이제 두 각의 이등분선에 대한 대수식을 같다고 하고, 방정식을 간단히 정리하면 두 인수의 곱이 0인 식이 된다. 두 인수 중에 하나는 반드시 0이 아니어야 남은 인수가 0이 될 수 있다. 그러나 남은 인수가 0이 될 수 없는 이유를 밝히지 않으면 이것은 직접 증명이라고 할 수 없다.
존 콘웨이(John Conway)는 같음으로 보이는(equality-chasing) 증명은 있을 수 없다고 주장했다. 왜냐하면 대수적으로 제시된 정리는 임의의 체 위에서 심지어 음의 실수가 길이로 허용되어도 성립하지 않기 때문이다.
그러나 누군가가 직접 증명이 무엇인지에 대하여 정확한 정의를 고안할 때까지는 논쟁거리로 남을 것이다.
그렇다. 직접 증명으로 해결하지 못한 이유가 있었다. 귀류법을 사용했어야 했다. 그러나 다시 풀기 귀찮아져서 여러가지 풀이를 찾을 수 있었다. 그 중에서 내가 처음에 생각했던 방향과 유사한 풀이를 소개하고 나머지는 링크로 대신한다. 참고로 직접 증명을 위한 여러 시도들도 함께 찾을 수 있었는데, 그 중에 기억에 남는 하나도 같이 링크로 대신한다.
한 가지 짚고 넘어 갈 것은, 첫 번째 링크에서 1~6번 방법과 두 번째 링크의 방법은 모두 삼각함수를 이용한 풀이인데 이 풀이를 대강만 봐도 저자가 쉽다고 말한 것이 정말 저자의 주관적인 생각임을 알 수 있다.
그리고, 기하학을 이용한 풀이 중에서는 첫 번째 링크에서 일곱 번째에 있는 A. I. Fetisov의 풀이와 여덟 번째에 있는 G. Gilbert와 D. MacDonnell의 풀이는 꼭 한 번 보길 바란다.
이제 세 번째 링크에 있는 B. Hagan의 풀이를 보자.
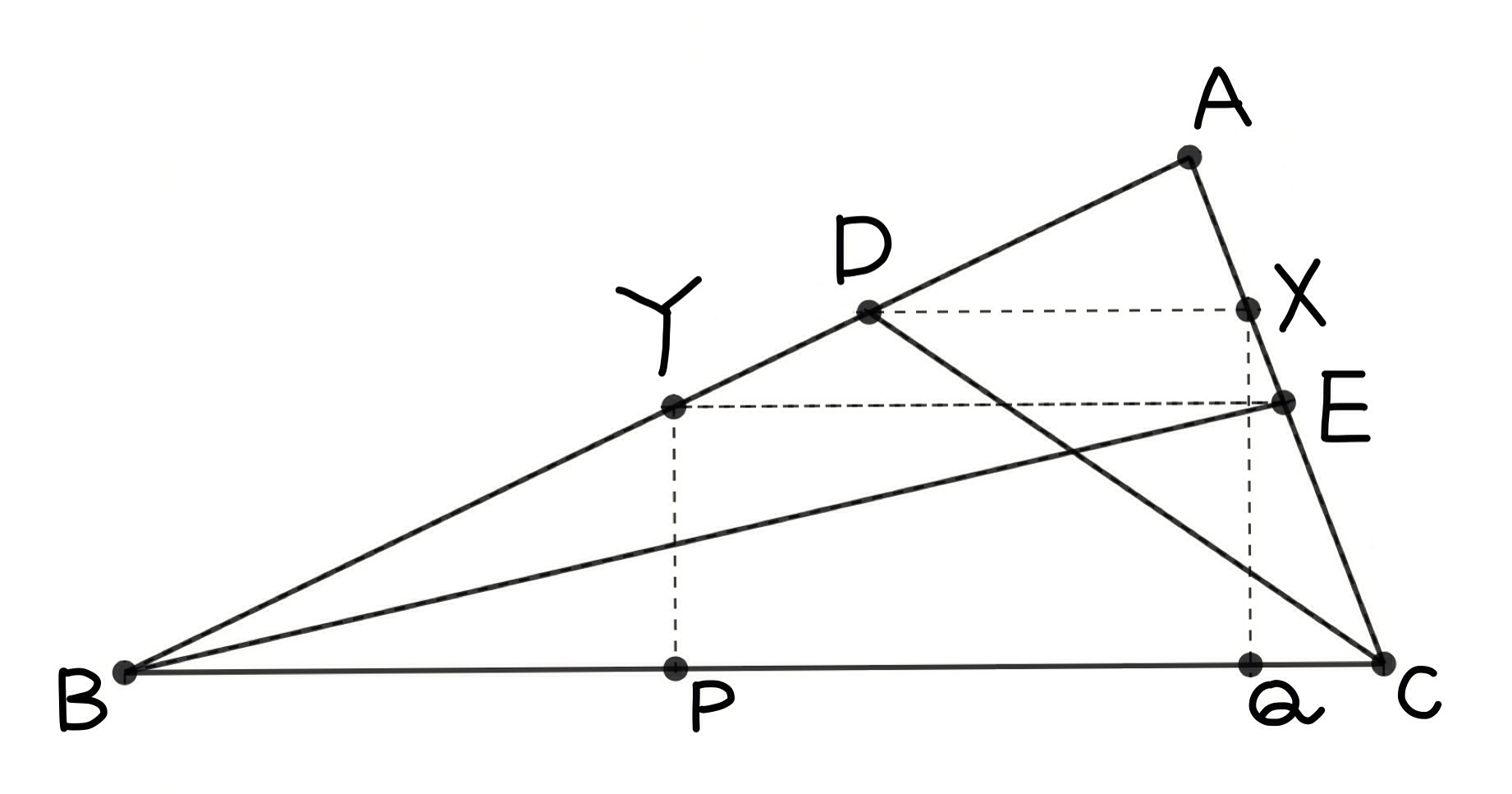
BE = CD 일 때, ∠B < ∠C 라고 가정하고, 점 D, E에서 BC에 수선을 내려 그 교점을 각각 P, Q라 하자.
그러면 빗변의 길이가 같은 두 직각삼각형 ⊿CDP, ⊿BEQ에서 ∠EBQ = ½∙∠B < ½∙∠C = ∠DCP 이다. 따라서, EQ < DP 이다.
이제 점 D, E에서 BC에 평행하게 각각 선분 DX, EY를 그리자. EQ < DP 이므로 DX < EY가 성립한다. 한편, △YBE를 주목하자. ∠YBE = ½∙∠B 이고, ∠YEB와 ∠EBC는 엇각으로 같다. 따라서 ∠YBE = ∠YEB 이다. 즉, △YBE는 이등변삼각형이다. 비슷하게 △XDC도 이등변삼각형이다.
이 때, BE = CD 이므로 두 이등변삼각형 △YBE와 △XDC의 밑변의 길이는 서로 같다. 그런데 ∠B < ∠C 이므로 EY < DX 이다. 이는 분명히 DX < EY 임에 모순이다.
∠B > ∠C 일 때도 위와 비슷하게 모순이 되므로 ∠B = ∠C 이다. 즉, △ABC는 이등변삼각형이다. ∎
