2014년 1월 21일에 작성한 텀블러 포스트이다.
'주어진 위치의 모든 나사를 조을 수 있는 로봇 팔을 설치할 위치와 로봇 팔의 길이에 관한 문제'를 제대로 이해하기 위해서 좀 과하게 이것 저것 찾아보던 중에 Hans Rademacher와 Otto Toeplitz의 책 《The Enjoyment of Mathematics》(1957)에 이 문제와 관련된 주제인 The Spanning Circle of a Finite Set of Points가 있음을 알게 되었다. 불행히도 번역서 《수학의 향연》을 구할 방법이 없었기에 직접 번역하였다.
§1. 평면 위의 n개의 점 P1, P2, ⋯, Pn으로 구성된 유한 집합 S를 생각해보자. 우리는 임의의 두 점 Pi, Pj 사이의 거리는 측정할 수 있다. 측정된 거리의 집합1에는 반드시 최대 거리가 존재하는데, 이 최대 거리는 점의 집합의 '최대거리'(span)라고 불린다.
S의 최대거리가 d일 때, n개의 점을 완전히 둘러싸는 반지름 d인 원을 다음과 같이 그릴 수 있다.
n개의 점 중에서 임의로 중심을 택하여 그리면 되는데, P1을 택하자. P1과 다른 모든 점 사이의 거리는 d 이하이므로 원은 P2, ⋯, Pn을 둘러싼다.
그런데, 모든 점을 둘러싸는 더 작은 원을 만드는 것은 간단하다.
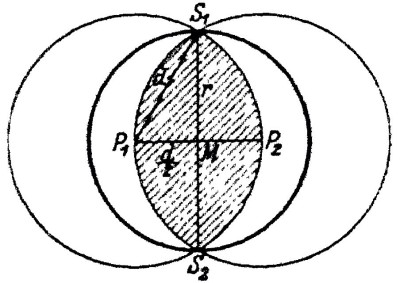
먼저 d만큼 떨어진 한 쌍의 점을 찾자. 만약 이러한 쌍이 여럿이면 아무거나 택하자. 선택한 점을 P1, P2라 하고, 각 점을 중심으로 반지름 d인 원을 그리자. 중심이 P1인 원은 P2를 지나고 반대 경우도 마찬가지다. S의 모든 점은 각각의 원에 둘러싸이므로 두 원의 공통 부분 즉, 위 그림의 빗금친 영역에 놓여 있다. 만약 두 원이 S1과 S2에서 만나면, 선분 S1S2를 지름으로 하는 원은 공통 부분을 둘러싸므로 모든 점을 둘러싼다. 그리고 새로운 원의 반지름 r는 △P1MS1에 피타고라스의 정리를 적용하여 얻는다.
r² = d² - (d/2)² = (¾)d².
집합 S의 모든 점을 둘러싸는 원을 S의 '동봉'(enclosing)2원이라 하면, 원래 동봉원의 반지름 r = d이고 새로운 동봉원의 반지름 r = (√3/2)d = 0.866⋯d.
§2. √3/2은 더 작은 수로 교체될 수 있을까? 이 물음에 대한 답은 독일의 수학자 융3에 의해 발견된 다음의 정리이다 : 유한개 점의 집합의 최대거리가 d이면 반지름이 d/√3 = 0.577⋯d 보다 크지 않은 동봉원을 갖는다. 더 작은 동봉원을 가진 유한 점 집합은 많지만 어떤 유한 집합들은 d/√3이 반드시 필요하다.4 반면에, 두 점은 동봉원의 지름 2∙r 보다 멀리 떨어질 수 없으므로 2∙r ≥ d 이다. 따라서 동봉원의 반지름은 d/2 보다 절대 작을 수 없다. 융의 정리의 증명이 바로 이 장의 목표다.
반지름이 d/√3인 동봉원은 한 변의 길이가 d인 정삼각형의 형태로 이루어진 세 점의 집합에서 쉽게 찾을 수 있다. 이것은 정삼각형의 외접원이다.

정삼각형에 대하여 외접원이 가능한 가장 작은 동봉원임은 분명하다.5 그러나, 이는 특수한 경우이므로 여기서 머무를 수는 없다.
§3. 융의 정리를 증명하기 위해서는 임의의 유한 점 집합에 대한 모든 동봉원 중에서 가능한한 작은 반지름을 가진 원을 택해야 한다. 계속하여 작은 동봉원을 찾게 하는 순차적인 단계를 살펴보자.
Ⅰ. 유한개 점의 집합 S의 점이 원주 위에 없는 동봉원 C1은 더 작은 동봉원 C2로 교체될 수 있다. C1과 같은 중심 M을 갖고 M과 거리가 가장 먼 S의 점(또는 점들)을 지나는 원 C2를 그릴 수 있기 때문이다.
Ⅱ. 만약 동봉원 C3위에 S의 딱 한 점만 있다면, 이 원은 더 작은 원으로 교체될 수 있다.

C3의 원주 위에 딱 하나 있는 S의 점을 P1이라 하자. P1에서 C3의 접선과 같은 접선을 가지면서 S에 있는 P1과 다른 점을 지나는 모든 원을 그리자.6 이 원들은 모두 C3안에 있다. 이 원들 중 가장 큰 원을 C4라고 하자. P1이 C3의 원주 위에 있는 S의 유일한 점인 반면에 C4의 원주 위에는 S의 또 다른 점이 있으므로 C4는 C3와 분명히 다르다. 이제 C4는 모든 새로운 원를 둘러싸고 따라서 S의 모든 점도 둘러싼다. 더군다나 C4에는 원주 위에 적어도 두 점이 있고, C3보다 작다.
Ⅲ. 동봉원의 원주 위에 놓인 S의 점들은 원주을 몇 개의 호로 나눈다. 간결한 설명을 위해 이러한 호 중에서 호의 양 끝점을 제외하고 호 위에 S의 점이 없는 호를 '면점'(point-free)7이라 하자. 원을 줄이는 세 번째 단계는 다음과 같다 : 만약 동봉원 위의 면점 호가 반원 보다 크면 동봉원은 더 작은 원으로 교체될 수 있다.8
S의 두 점 P1과 P2를 동봉원 C5에 대한 면점 호 b의 양 끝점이라고 하자. 더욱이 b는 반원 보다 크다. 현 P1P2를 지름으로 하는 원 C∗를 그리자.

만약 C∗가 S의 모든 점을 둘러싸고 있으면, C∗는 C5보다 작은 동봉원이다. 다시말해 현 P1P2는 C5의 지름이 아니므로 (그렇지 않으면 b는 반원이다.) C5는 반드시 C∗보다 크다. C∗가 S의 모든 점을 둘러싸지 않으면 남는 점들은 b와 C∗사이의 반달모양으로 빗금쳐진 영역에 존재한다. b는 면점 호이므로, P1과 P2 이외의 S의 점은 b 위에 없다. 이제 P1, P2, 반달모양 영역에 있는 S의 점을 지나는 가능한 모든 원을 그리자. 이러한 각각의 원들의 C5 안쪽 부분은 반달모양 영역에 있게 되므로 C∗ 바깥쪽에 있고, C∗ 안쪽 부분은 C5 바깥쪽에 있다. 위에서 그린 원들 중에서 반달모양 영역에서 현 P1P2로 부터 가장 멀리 있는 호를 가진 원을 C6 이라고 하자. 이 원은 반달모양 영역에 있는 S의 모든 점을 둘러싸므로 S의 모든 점을 둘러싼다. 더욱이 C6은 C5보다 작다. 왜냐하면 C6의 원주는 C5와 C∗사이에 있으므로 C5보다 중심이 현 P1P2에 가깝기 때문이다.
동봉원이 Ⅰ, Ⅱ, Ⅲ의 방법으로 더 줄어들지 않으면, 이 원에는 반원 보다 큰 면점 호가 없는 것이다. 이러한 원은 반드시 S의 두 점을 지름으로 갖거나, S의 세 점 혹은 더 많은 점들에 의해 원주가 반원 보다 작은 호로 나뉘어 있다. 전자의 동봉원을 '지름(diametric)원'이라 하고, 후자는 '세점(three-point)원'이라고 부르자. Ⅰ, Ⅱ, Ⅲ에 적용된 임의의 동봉원은 반드시 두 가지 경우 중 하나에 속한다. 두 경우에 동시에 속할 수도 있는데 예를 들면 동봉원이 사각형의 네 꼭지점을 지나는 것이다.
§4. 이제 유한 집합 S의 두 점을 지름의 양 끝으로 하는 원뿐만 아니라, S의 세 점을 지나는 가능한 모든 원을 생각하자.9 이 모든 경우의 원이 동봉원이 되는 것은 아니지만, 그러한 경우에는 모든 지름 원과 세점 원이 속한다. 전체 경우의 수가 유한하므로 지름 원과 세점 원의 수도 유한하다. 그러므로 모든 지름 원과 세점 원을 비교하여 가장 작은 원을 택할 수 있다. 선택된 원 c가 가장 작은 동봉원이다. c는 Ⅰ, Ⅱ, Ⅲ에 의해 모든 지름 원과 세점 원 중에서 최소이므로 다른 어떤 동봉원 보다도 작다.

더욱이 이것은 유일하다. 크기가 같은 다른 동봉원 c′이 있다면, S의 모든 점은 c′에 둘러싸이면서 c에도 둘러싸인다. 그러면 S의 모든 원소는 두 원의 공통 부분에 둘러싸여 있다. 공통 부분은 더 작은 원 c∗에 의해 둘러싸이기 때문에 c의 최소성에 위배된다. 이처럼 유한 집합 S의 유일하게 결정된 가장 작은 동봉원을 유한 집합 S의 '최소동봉원'(spanning circle)이라고 부를 것이다. 최소동봉원 c는 Ⅲ에 의하여 반원 보다 큰 면점 호를 가질 수 없다.
§5. 이제 최소동봉원 c의 반지름이 d/√3 보다 크지 못함을 보일 것이다. 이를 위해 c의 원주 위에 있는 S의 한 쌍의 점 중에서 다른 어떤 쌍 보다 서로 멀리 떨어진 쌍을 택하자. 그러한 쌍의 두 점 사의 거리 δ는 분명히 S의 최대거리 d 보다 클 수 없다.
첫째, 지름 원인 경우에 c의 지름 2∙r = δ ≤ d 이다. 따라서 r ≤ d/2 이고, 분명히 r < d/√3 이다.
둘째, 지름 원이 아닌 경우에 c의 원주 위의 가장 큰 면점 호 b를 택하자. 같은 크기의 이런 호들이 여럿 있으면 아무거나 택하자. b의 끝점 P1과 P2는 S의 점일 것이다. c의 면점 호는 반원 보다 클 수 없으므로 호 b는 반원 보다 작다. 만약 b가 반원이면, P1과 P2는 지름의 끝점이 되므로 첫째로 환원된다. 이제 현 P1P2를 그리고 현의 끝점에서 현에 대한 수직선을 그리자.

두 수직선은 서로 다른 두 점 Q1과 Q2에서 원을 자른다. Q1과 Q2에 의해 잘린 호 b′은 호 b의 반대편에 있고 크기가 같다. Q1, P2와 Q2, P1은 각각 지름의 끝점이 되므로 Q1과 Q2는 S에 속할 수 없다. 다시 말해, Q1 또는 Q2가 S에 속하면 첫째로 환원된다. 한편, 호 b′은 면점이 아니다. 호 b′이 면점이면 b′은 S에 없는 두 점 Q1과 Q2를 넘어 더 큰 면점 호로 확장될 수 있다. 호 b 보다 큰 면점 호는 없으므로 이는 불가능하다.
결과적으로, 호 b′ 위의 Q1과 Q2 사이에 S의 점이 적어도 하나 존재한다. 이를 P3라 하자. 세 점 P1, P2, P3는 '예각삼각형'을 만든다. 그 이유는 다음과 같다. P1과 P2의 각은 P1과 P2에서 구성된 직각보다 작으므로 예각이다. 반원의 원주각은 직각이고, 더 작은 호는 더 작은 각에 대응한다. 따라서, P3의 각은 반원 보다 작은 호 b의 원주각이므로 예각이다.
c의 원주는 세 점 P1, P2, P3에 의해 세 호로 나뉜다. △P1P2P3는 예각삼각형이므로 세 호 중에서 길이가 적어도 원주의 ⅓이 되는 한 호가 반드시 존재한다. 그러한 호의 현 PiPj는 반드시 원주의 ⅓ 이상을 자른다. 다시 말해 현 PiPj는 원 c에 내접한 정삼각형의 한변의 길이 s 이상의 길이를 갖는다. 현 PiPj의 길이는 길어야 최대거리 d이기 때문에, s ≤ d 이다.
우리는 §2에서 한 변의 길이가 s인 정삼각형에 외접한 원의 반지름 r′은 s/√3와 같음을 보았다. 원 c의 반지름 r에 대하여 s ≤ d 이므로 r ≤ d/√3 이다. 이는 우리가 보이고자 한 것이다.
§6. 일반적인 유한 점 집합에 대하여 d/√3가 더는 작아질 수 없음을 밝혀야 한다. 정삼각형의 세 꼭짓점으로 된 집합 Ƭ에 §4의 방법을 적용하자.10 아래 그림에 Ƭ의 두 점을 지름의 끝점으로 하는 세 원과 Ƭ의 모든 점을 지나는 원이 그려져 있다.11

이 중에서 동봉원은 세 점을 모두 지나는 외접원뿐이다. 외접원과 비교할 다른 원이 없으므로 외접원이 최소동봉원이다. 정삼각형의 한 변이 Ƭ의 최대거리 d이므로 외접원의 반지름은 d/√3이다. 이 특별한 유한 집합이 반지름 d/√3인 최소동봉원을 가지므로 일반적인 유한 집합에 대하여 d/√3이 더 작아지는 것은 불가능하다.
여기서 우리는 외접원이 집합 Ƭ의 최소동봉원임을 밝히는데 §4를 사용했다. 외접원이 집합 Ƭ의 최소동봉원임은 마치 증명없이도 정당하고 명백하게 보이지만, 자명한 것이 아니다.

예를 들면, 둔각삼각형의 꼭짓점들의 최소동봉원은 외접원이 아니고 가장 긴 변을 지름으로 하는 원이다.
- 거리의 집합에는 nC2개의 원소가 있다. [본문으로]
- (역자 주) 번역서는 절판되었지만 목차 정도는 볼 수 있었다. 목차에서 ‘The Spanning Circle of a Finite Set of Points’을 ‘유한 집합과 최소동봉원에 대하여’로 번역해 놓은 것에 착안하여 이름 붙였다. [본문으로]
- (역자 주) Heinrich Wilhelm Ewald Jung [본문으로]
- (역자 주) 가장 작은 동봉원의 반지름이 d/√3일 수 있기 때문이다. 이는 §6에서 확인할 수 있다. [본문으로]
- (역자 주) 이 분명한 듯한 결과는 §6에서 그 이유가 명백하게 밝혀진다. [본문으로]
- (역자 주) P1이 아닌 S의 점 Pk에서 선분 P1Pk에 수직인 직선 ℓ1을 그리고, P1에서 접선과 수직인 직선 ℓ2를 그리고나서 ℓ1과 ℓ2의 교점 Q와 P1을 지름의 양 끝점으로 하는 원을 그리면 된다. [본문으로]
- (역자 주) ‘duty-free’를 일반적으로 면세라고 번역하는 것과 같은 방식으로 이름 붙였다. [본문으로]
- Ⅰ과 Ⅱ에서 원주 자체가 면점 호 이므로 Ⅰ과 Ⅱ는 Ⅲ의 특수한 경우로 볼 수도 있다. [본문으로]
- 많아야 nC2 + nC3개의 원이 있다. [본문으로]
- (역자 주) §4의 방법이란, 모든 지름 원과 세점 원을 비교하여 가장 작은 원을 택하는 것이다. 유한 집합의 두 점을 지름의 양 끝으로 하는 원 또는 세 점을 지나는 가능한 모든 원의 수가 유한하므로 지름 원과 세점 원의 수도 유한하기에 가능한 방법이다. 그리고 매우 기본적인(elementary) 방법이다. 사실 이렇게 기본적으로 셈을 가능하게 하는 것은 단계 Ⅰ, Ⅱ, Ⅲ의 기발한 방법 때문이다. [본문으로]
- (역자 주) §4의 방법에 의하면 가능한 모든 경우의 원의 수는 3C2 + 3C3 = 4이다. [본문으로]
