2014년 2월 6일에 작성한 텀블러 포스트이다.
아래는 영문 위키의 'Lagrange multiplier'의 내용을 바탕으로 쓴 글이다.
'수학적 최적화'(mathematical optimization)라는 분야에서, 라그랑주 승수법은 제약 등식(equality constraint)을 조건으로 갖는 함수의 극댓값과 극솟값을 찾는 전략이다.
예를 들어, 다음의 최적화 문제를 고려해보자.
g(x, y)=k 인 조건에서 f(x, y)를 최대화하라.1
이 전략에서 f와 g는 일계 편도함수가 연속이어야 한다. 이제 라그랑주 승수라고 불리는 새로운 변수 λ를 도입하고, 라그랑주 함수 또는 Lagrangian이라고 불리는 다음과 같이 정의된 함수를 살펴보자.
Λ(x, y, λ) = f(x, y) + λ·(g(x, y)-k)
여기서, 제약(constraint) 조건 g(x, y)=k 를 고려하는 기발한 방법은 g(x, y)-k = 0 으로 바꿔 쓰고, 0은 원하는 만큼 여러번 f에 더해도 f에 아무런 변화를 주지 않으므로 λ를 곱해 f에 더하여 얻은 윗 식 Λ가 최대가 되도록 하는 것이다.22
만약 f(x0 , y0)가 본래의 제약 조건에서 f(x, y)의 최댓값이면, Λ가 모든 변수에 대하여 편미분 가능하므로 (x0, y0, λ0)가 라그랑주 함수 Λ에 대한 임계점(stationary point)이 되는 λ0가 존재한다. 따라서 ∇Λ(x0, y0, λ0)=0 이다.
그러나 역으로 ∇Λ=0 이 되는 모든 임계점이 본래 문제의 해답이 되지는 않는다. 따라서, 라그랑주 승수법은 제한된 문제에서 최적화에 대한 필요조건을 찾는 것이다.
이제는 기하학적 의미를 통해 라그랑주 승수법을 알아보자.
c의 다양한 값에 대하여 f(x, y)=c 의 등치선(contour)을 그리고, 마찬가지로 주어진 g(x, y)=k 의 등치선을 그리자.
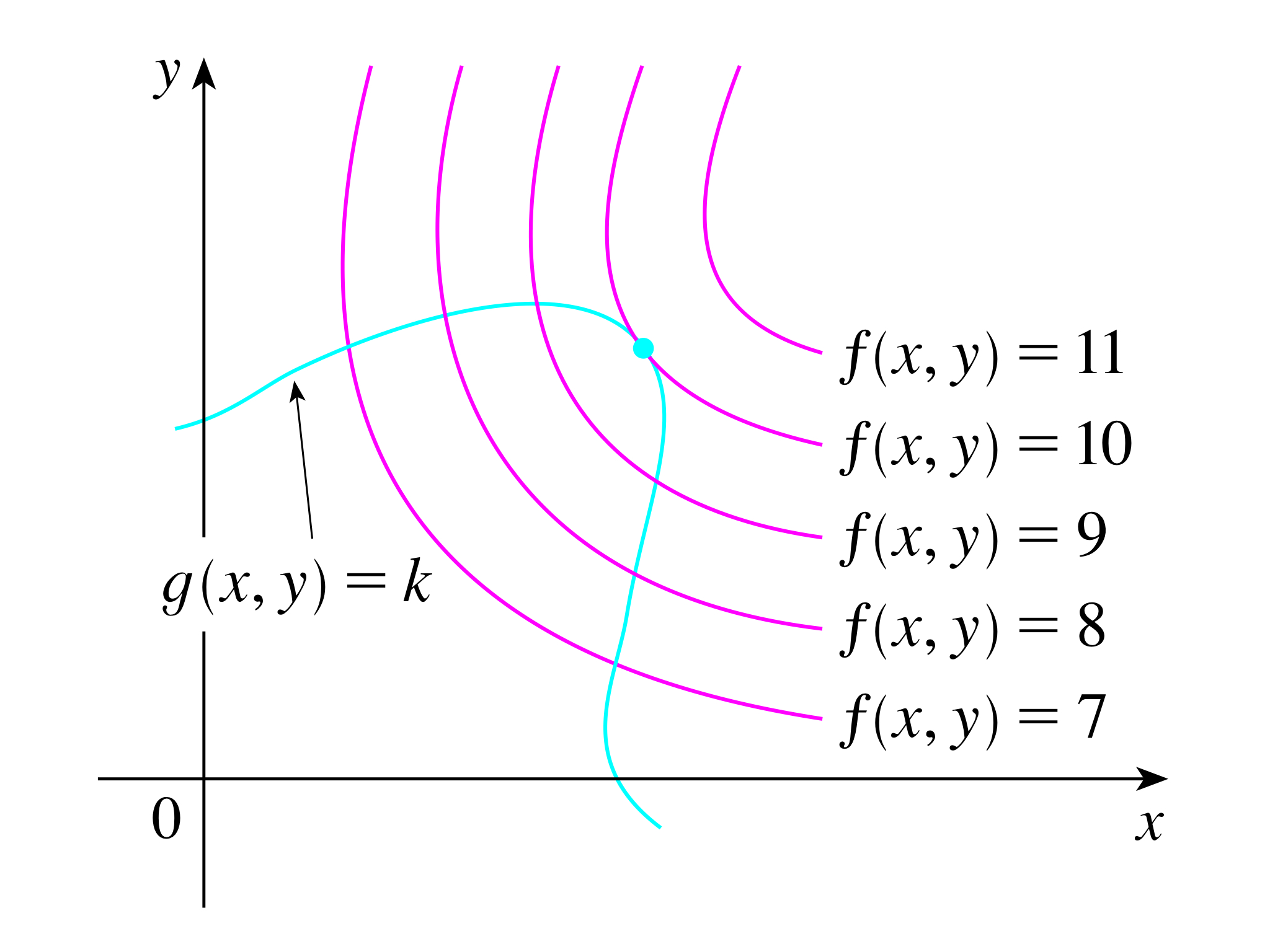
g=k의 등치선을 따라 걷는다고 해보자. 일반적으로 f와 g의 등치선은 서로 다르다. 따라서 g=k의 등치선을 따라 걷다보면, f의 등치선을 가로지르게 된다. 이는 g=k의 등치선을 따라 이동하는 동안 f의 값이 달라진다는 것과 같은 의미이다.
오직 g=k의 등치선과 f의 등치선이 접할 경우에만, f의 값은 증가하거나 감소하지 않는다. 즉, 두 등치선이 접하면, 서로 가로지르지 않는다.
등치선의 접벡터가 서로 평행할 때, f와 g의 등치선이 접한다. 함수의 기울기(gradient) 벡터는 등치선과 수직이므로, f와 g의 기울기 벡터가 서로 평행할 때를 찾아도 좋다. 따라서, g(x, y)=k 이고, ∇f = -λ∇g 를 만족하는 (x, y)를 찾으면 된다.
단, 여기서 기울기 벡터 ∇f=(∂f/∂x, ∂f/∂y) 이고, ∇g=(∂g/∂x, ∂g/∂y) 이다.
그리고 두 기울기 벡터는 평행하기만 하면 되고 길이는 같을 필요가 없으므로, 상수 λ가 요구된다. 이러한 조건들을 한 방정식에 씀으로서, 다음과 같은 보조 함수를 도입할 수 있다.
Λ(x, y, λ) = f(x, y) + λ·(g(x, y)-k)
그리고나서 ∇Λ(x, y, λ) = 0 를 풀면 된다. 특히, ∂Λ/∂λ=0 는 g(x, y)=c 를 함의한다는 점에 주목하자. 한편, f의 제한된 극값은 라그랑주 함수 Λ의 임계점이지만, Λ의 모든 임계점이 Λ의 극값이 되는 것은 아니다.
참고 목록
- Constrained Optimization
- Karush-Kuhn-Tucker conditions: 라그랑주 승수법의 일반화된 방법
