2014년 3월 19일에 작성한 텀블러 포스트이다.
영문 위키의 'Hasse diagram' 페이지에서 4차 정이면체군(Dihedral group) D4에 대한 굉장히 직관적인 Hasse diagram을 봤다.

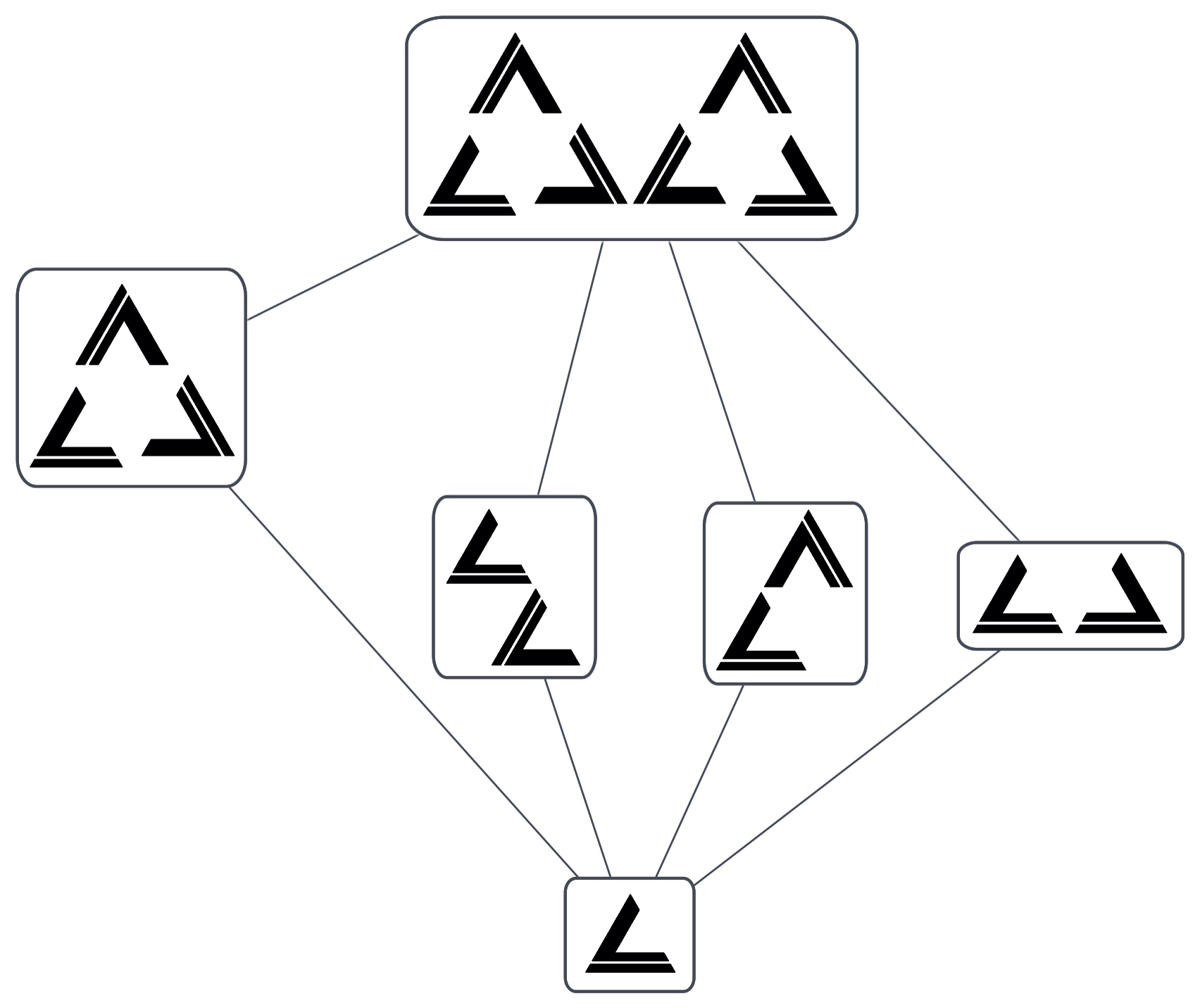
4차 정이면체군 D4를 시각적으로 표현한 방법이 굉장히 직관적이기 때문에 D4를 단번에 파악할 수 있다. 3차 정이면체군 D3에 대해서도 이와 비슷한 시각적 표현법이 있을 것 같아서 구글링을 해봤지만, 아쉽게도 찾을 수 없었다. 그래서 직접 만들었다.
Geometer's Sketchpad와 Windows7의 그림판 그리고 iOS 응용프로그램 Grafio Lite를 이용하여 그렸다.
위와 같은 그림을 생각하게된 것은, D3가 3차 대칭군(Symmetric group) S3와 동형이기 때문이다. 정삼각형의 세 변을 각각 1, 2, 3이라 하자. 2를 이중선으로 바꾸고 3을 지우자.1 한 변을 지워도 남은 두 변이 연결되어 있으므로 바뀐 삼각형을 보고도 삼각형의 세 변이 1, 2, 3에 대응되어있다는 것을 쉽게 확인할 수 있다.
이쯤에서 n차 정이면체군을 되돌아보자.
n차 정이면체군 Dn을 보통 다음과 같이 표현한다.
Dn=<σ, τ | σn=τ2=1, τ−1στ=σ−1>
단, σ는 정n각형을 반시계 방향으로 360°/n 만큼의 회전이동하는 회전변환이고, τ는 정n각형의 n개의 대칭축 중에서 어떤 하나의 대칭축에 대하여 선대칭하는 대칭변환이다.
특히, 항등식 τ−1στ = σ−1 의 의미를 물리적으로 해석할 수 있다. 작은 구멍이 촘촘히 뚫린 종이벽에 쇠로 만든 정n각형을 붙였다고 생각하자(중력은 무시하자!). 그리고 정n각형을 반시계 방향으로 회전시킨다고 하자. 벽면의 반대편에서 보면 정n각형은 분명히 시계 방향으로 회전할 것이다.
이제 τ를 벽면의 반대편으로 건너가서 정n각형을 관찰하는 행동으로 간주하고, σ를 정n각형을 반시계 방향으로 360°/n 만큼의 회전하는 행동으로 간주하자.
그러면, τ−1στ는 벽면의 반대편으로 건너가서 (자석을 이용하여) 정n각형을 반시계 방향으로 360°/n 만큼의 회전이동하고 다시 원래 자리로 돌아와서 정n각형을 관찰함을 뜻한다.
벽면의 반대편에서 반시계 방향으로 360°/n 만큼의 회전하였으므로 분명히 원래 자리로 돌아와서 보면 시계 방향으로 360°/n 만큼의 회전되었을 것이다. 즉, σ−1의 뜻과 같다.
3차 정이면체군에 대한 시각적 표현을 그림 아래의 설명과 같이 생각할 수 있다.

- D3로 볼 경우에, 윗줄은 차례로 항등변환 1 = σ3, σ, σ2에 대응되고 아랫줄은 차례로 τ, στ, σ2τ에 대응된다.
- S3로 볼 경우에, 윗줄은 차례로 항등변환 1, (1 2 3), (1 3 2)에 대응되고 아랫줄은 차례로 (1 2), (1 3), (2 3)에 대응된다.
- 투명선으로 바꾼다고 생각해도 좋다. [본문으로]
