정다각형이란?
우리나라의 2015 개정 교육과정에서 정다각형은 초등학교 4학년 2학기에 다음과 같이 소개된다.
변의 길이가 모두 같고, 각의 크기가 모두 같은 다각형을 정다각형이라고 합니다.
이 뜻에 비추어 아래의 도형은 정다각형이 될 수 있는지 살펴보자.
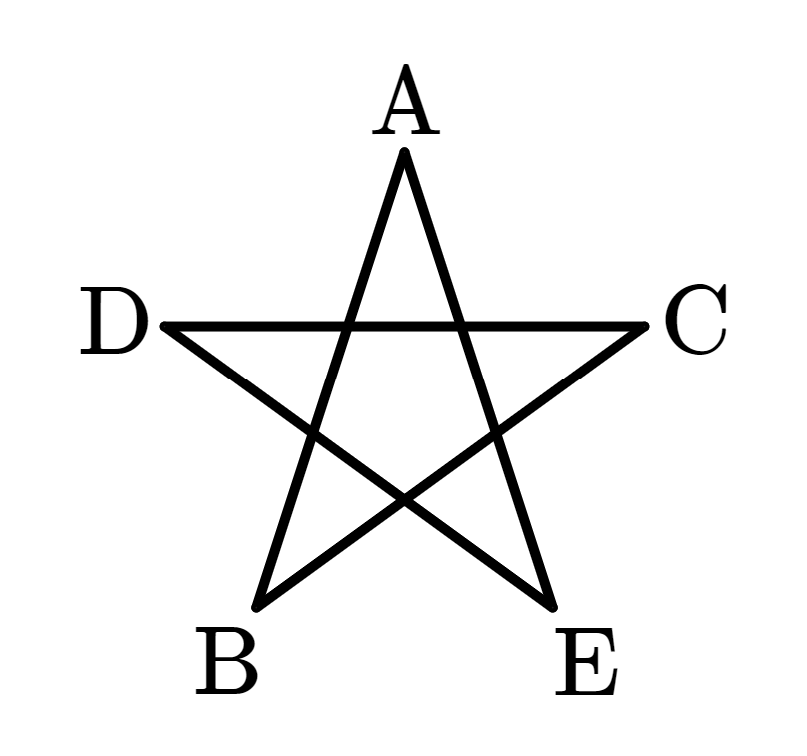
- 이 도형에서 변과 변이 겹치는 것을 무시하면, 꼭짓점이 다섯 개이고 변이 다섯 개라고 볼 수 있다.
- 이제 오각별 ABCDE의 다섯 변의 길이가 모두 같다고 하자.
- 또한 다섯 각의 크기가 모두 같다고 하자.
- 그러면, 이 오각별은 정오각형의 뜻에 맞다. 따라서, 위 조건을 만족하는 오각별은 정오각형이다?!
- 정오각형이라는 말에 해당하는 도형이 둘이나 되면 곤란하므로, 위 조건을 만족하는 오각별을 정오각별이라하자.
일반화된 정다각형
- 우리가 학교에서 배우는 정다각형은 사실 단순 다각형(Simple polygon)이면서도 볼록 다각형(Convex polygon)이다.
- 단순 다각형이란, 겹치는 변이 없는 다각형이라는 뜻이고,
- 볼록 다각형이란, 오목한 부분이 없는 다각형이라는 뜻이다.
- 학교에서 다각형의 단순성과 볼록성을 다루기는 복잡하기 때문에 정다각형을 말할 때, 단순성과 볼록성은 별도로 언급하지 않을 뿐이다.
- 그런데 학교에서 말하는 정다각형의 뜻으로만 보면 정다각별(Regular star polygon)도 정다각형이라 할 수 있다.
- 이제 정다각형을 정다각별을 포함한다고 하고, 정다각형의 몇 가지 성질을 살펴보자.
한 외각의 크기(°)에 따라 정해지는 일반화된 정n각형
- 위 그림은 한 외각의 크기가 1°부터 179°인 일반화된 정다각형을 차례대로 나열한 것이다.
- 빨간색은 정다각형, 회색은 정다각별이다.
- 색이 뚜렷할수록 변의 개수가 적고, 색이 흐릴수록 변의 개수가 많다.
- 한 외각의 크기가 k°일 때, 몇 개의 변이 있어야 일반화된 정다각형이 될까?
단, k는 180미만의 양의 정수라 하자.
다각형의 외각 크기의 합
위 질문에 대한 답은 외각의 크기의 합을 통해 알 수 있다. 다각형의 외각 크기의 합 실험으로 알아보자.
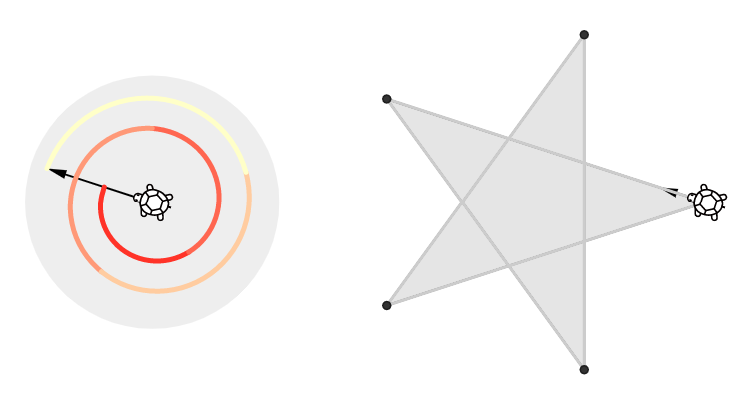
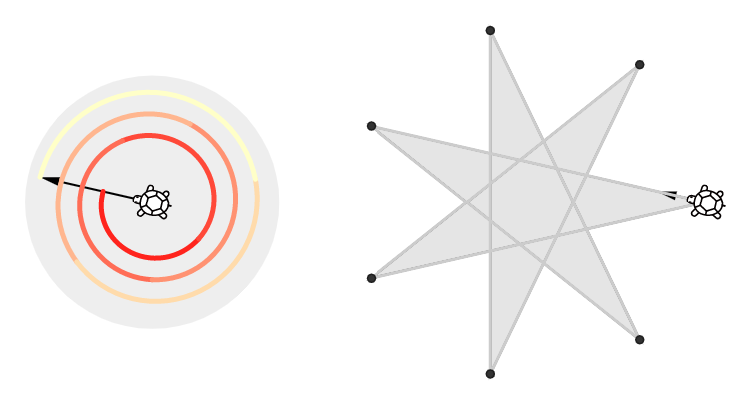
- 예를 들어, 그림3과 같은 정오각별에서 외각의 크기의 합이 360°×2이고,
그림4와 같은 정칠각별에서 외각의 크기의 합은 360°×3이다. - 실험에서 다각형의 외각 크기의 합은 거북이의 회전각의 합과 같다.
- 거북이가 다각형의 한 꼭짓점에서 출발하여 둘레를 따라 제자리로 돌아와 처음 가리켰던 방향을 가리키는 과정에서
- 거북이의 회전만 보면 돌고 돌아 처음 가리킨 방향을 가리켜야 하므로
- 회전각의 합은 360°의 배수가 되어야 한다.
- 따라서, 다각형의 외각 크기의 합은 360°의 배수가 되어야 한다.
한 외각의 크기가 k°일 때, 필요한 변의 개수
- 다각형의 외각 크기의 합은 360°의 배수가 되어야 하므로
한 외각의 크기가 k°일 때, k×n이 360의 배수가 되는 n개의 변이 있어야 일반화된 정다각형이 된다. - 이러한 n은 무수히 많은데, 그 중에서 가장 작아야 한다. 그렇지 않으면, 같은 변을 여러 번 그리게 된다.
- 다시 말해, k×n은 k와 360의 최소공배수가 되어야 한다.
- 최소공배수와 최대공약수의 성질을 이용하면, 이러한 n은 360을 k와 360의 최대공약수로 나눈 몫임을 알 수 있다.
- 예를 들어, 다음과 같다.
- 한 외각의 크기가 5°일 때, 72개의 변이 필요하다.
- 한 외각의 크기가 6°일 때, 60개의 변이 필요하다.
- 한 외각의 크기가 7°일 때, 360개의 변이 필요하다.